Da ispišem rešenje pa možete da me kamenujete. :)
Lema:
Neka su
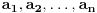
pozitivni realni brojevi i neka je
primitivan
-ti koren jedinice, tj.
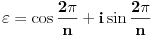
. Ako stranice mnogougla sa jednakim uglovima imaju dužine
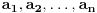
(u smeru suprotno kazaljci na satu), onda je:
.
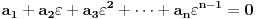
Dokaz:
Neka su stranice mnogougla vektori orijentisani u smeru suprotnom kazaljci na satu (na slici je prikazan primer za
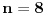
). Tada je suma ovih vektora jednaka nuli. Translirajmo sve vektore tako da imaju zajednički početak
. Ako sada zamislimo da se nalazimo u kompleksnoj ravni, vidimo da su tačke kojima odgovaraju ovi vektori upravo
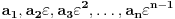
, redom. Sledi tvrđenje leme.
Možemo još zapaziti da obrnuti smer ne važi uvek što vidimo, recimo, na primeru paralelograma. Ipak, na osnovu dokaza zaključujemo za pozitivne realne brojeve
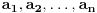
takve da važi
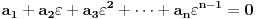
uvek postoji mnogougao sa jednakim uglovima čije su to stranice (tim redom).
Sada možemo preći na tvrđenje zadatka.
Dovoljno je dokazati da postoji polinom
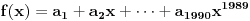
takav da su
brojevi
u nekom poretku i da je
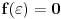
za
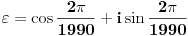
. Drugim rečima, pokazujemo da postoji permutacija
brojeva
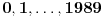
takva da je
.
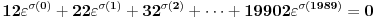
Za proizvoljan prirodan broj
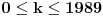
definišimo preslikavanje
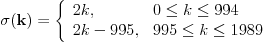
Lako se proverava da je ovako definisano preslikavanje, po modulu
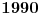
, zaista permutacija brojeva
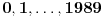
. Proverimo ispunjava li željene uslove.
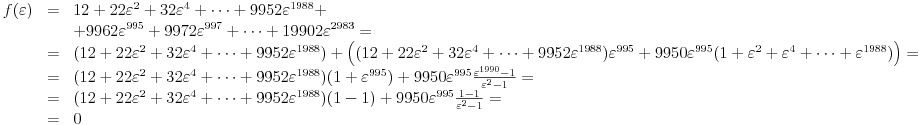
Ovim je zadatak rešen, a sad brzo bežim da ne bih čuo komentare. ;) Šalim se, naravno, kao i uvek ću vrlo rado primiti eventualne kritike i/ili pohvale, i razrešiti nedoumice.
Ljubičice crvena, što si plava kô zelena trava.
Vrlo tezak zadatak
Registrovani: 8 ( Bojan Basic, petkons, B3R1, Ultrena, sabosim, BoJaNa Brb, 33rf, Nebojsa Milanovic )