Citat:
Bojan Basic: Što se tiče Gedelovih teorema, to što si rekao jeste tačno ako posmatraš iz ugla shvatanja matematike Međutim, ako posmatramo sa druge strane, to je samo još jedna teorema na kojoj se temelji dalji razvoj, a takvih ima mnogo u svim vremenima (istina da je ovo jedna od najznačajnijih 20. veka, ali i dalje je samo teorema). No, za hipotezu kontinuuma definitivno ne shvatam šta želiš da kažeš - svojevremeno je dokazano da je ona nedokaziva, i preostaje samo da se ljudi dogovore i kažu: "Da, hoćemo je prihvatiti" ili: "Ne, nećemo je prihvatiti". Vudinov rad je još jedan argument u korist neprihvatanja koji je uključio neke stvari koje se do sada nisu vezivale za hipotezu kontinuuma, ali i dalje je samo argument koji će eventualno da prethodi generalnom konsenzusu.
Ako tako gleda[ na stvari, nikada se ni[ta nije promenilo. Epohalna su upravo ona otkrića koja su menjala ljudska shvatanja nečega, kao i ostala koja su donela potpuno nove ideje. a ne samo što su rešavala neki partikularan problem. Tu recimo spadaju otkriće nesamerljih duži kod starih grka, zatim otkriće infinitezimalnog, diferencijalnog i integralnog računa, otkriće Galoaove teorije, otkriće neeuklidskih geometrija i da ne nabrajam više.
Što se tiče kontinuum hipoteze, ona je rešena samo u formalističkoj formulaciji. Utvrđen je njen status u jednoj formalnoj teoriji - ZFC. Sada se postavlja pitanje kako protumačiti.
Stanovište da je nesaznatljivo sve ono što je neraspravljivo u ZFC je neprihvatljivo. Prema Gedelovoj teoremi nepotpunosti je Con(ZFC) neraspravljivo u ZFC, pa ipak smatramo da je Con(ZFC) faktički tačno. Niko ozbiljan neće odvaciti hipotezu Con(ZFC) u korist njene negacije. Tako i pitanje koliki je kontinuum. Neraspravljivo je sredstvima ZFC, ali to i dalje ne znači da je odgovor nesaznatljiv. Vudinov članak ide u pravcu prihvatanja novih sredstava (
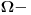
logika) koja su prihvatljiva, a pomoću kojih je moguće rešiti problem kontinuuma.
Kada govorim o prihvatljivosti, pre svega mislim na to da je Con(ZFC) prihvatljivo za razliku od negacije od Con(ZFC) i na to da aksiome teorije skupova nisu slučajno baš takve. One odražavaju neka svojstva skupova za koja se nama "čini" da su tačna, pa ih prihvatamo u daljem izučavanju teorije skupova i matematike uopšte. Mogle su aksiome da budu neki levi nizovi znakova. Sa formalističke tačke gledišta bi podjednako imalo smisla izučavati i takve formalne sisteme. Međutim, ljudi ipak znaju zašto su izabrali baš te formule za aksiome.
Citat:
Bojan Basic: Svakako da neće oni biti vođe daljeg razvoja, ali ima primera kada su dosta doprineli. Primera radi, C. Reiher (tada bio na kraju srednje škole) je 2003. godine potpuno sam dokazao Kemnitzovu hipotezu, jedan od bitnijih problema iz aditivne teorije brojeva star 20 godina.
Mislim da je Galoa mnogo bolji primer. On je sa 17 godina rešio jedan od najznačajnijih problema tadašnje matematike, i napravio jednu od najvećih revolucija u istoriji matematike odlepivši je od shvatanja kao "nauke o brojevima i prostornim odnosima". Gaus je sa 19 godina rešio problem konstruktibilnosti pravilnih poligona lenjirom i šestarom. Ipak, u najvećem broju slučajeva velike prodore pravili oni koji su mnogo naučili pre toga. Dakle, ne tvrdim da tako nešto nije moguće, već da su to samo vrlo retki izuzeci koji potvrđuju pravilo.
Citat:
Bojan Basic: Ovde bi se takođe moglo polemisati, ali pošto su "mnogo primera" i "teški problemi" vrlo relativni pojmovi ne verujem da bi diskusija oko toga daleko stigla. Jedino što, u vezi sa ovim, mogu da preporučim (ne Nedeljku, nego svima) odličnu knjigu Proofs from THE BOOK koja je sakupila mnoštvo takvih dokaza.
Upotrebio sam relativne pojmove da bih se jednim delom ogradio od bukvalnih tumačenja moje izjave. Naravno da takvih primera ima, ali opet, u moru drugih teških problema čije rešavanje je zahtevalo upotrebu vrlo složenih aparata to su samo izuzeci koji potvrđuju pravilo.
Citat:
Bojan Basic: Kao što rekoh, dokaz je dokaz a metod koji je u njemu korišćen je manje bitan. "Cilj ne bira sredstvo".
Sa ovim se duboko ne slažem. Često je metod korišćen
mnogo važniji od samog konačnog rezultata. Jedan od najboljih primera je velika Fermaova teorema. Daleko manje je značajan konačan rezultat od svog onog matiša koji je uveden u pokušajima da se ona reši. Iz XIX veka nam je ostala Kumerova teorija prstena i ideala, a iz XX veka važni delovi algebarske geometrije. Takođe, Gedelov konstruktibilni univerzum i Koenov metod forsinga su važniji od činjenice da kontinuum hipoteza ne zavisi od ZFC aksioma, ili činjenice da aksioma izbora ne zavisi od ostalih aksioma teorije skupova. Takođe, važnije je što se matematika odlepila od onoga što neki ciniočno zovu "prebrojavanjem ovaca na livadi", od samog rešenja problema rešivosti algebarskih jednačina preko radikala. Ideje, ako su velike i nove, obično daju plodove ne samo u rešavanju onog problema čijim se rešavanjem došlo do tih ideja, već i u rešavanju mnogih drugih problema.
Nije bitno koji su zaključci izvučeni, već kako se do njih došlo.