Evo, neću da pravim nikakvu nauku od toga, sve je vrlo jednostavno.
Ako imamo zadato prvih n članova treba da sastavimo kako nam god padne na pamet sistem od n-2 jednačine sa n-2 nepoznate (zbog toga što prva su prva dva broja nezavisna, a svi ostali prema hipotezi se mogu dobiti od njih, rekurentno). Tada samo rešimo sistem i dobijemo koeficijente koji figurišu u rekurentnoj formuli, onda odaberemo drugi sistem i dobijemo drugu rekurentnu formulu, itd. Npr., na srkijevom primeru to izgleda ovako:
Lupetanje 1:
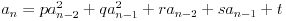
Jedino što treba paziti je da imamo n-2 (u ovom slučaju 5) nepoznate (to su p, q, r, s i t). U ovu jednačinu sam 5 puta uvrstio vrednosti koje je srki dao, i tako dobio sistem od 5 linearnih jednačina sa 5 rešenja, rešavanjem toga se dobije malopre napisana formula.
Lupetanje 2:
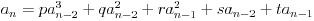
Na isti način dobijem drugačiji sistem koji ima drugačija rešenja, pa je i rekurzivna formula drugačija, i napisana je u mojoj prošloj poruci.
E sad, očigledno je da možemo puštati mašti na volju kako želimo, ali neko se ipak može zapitati postoji li ipak neka granica, a odgovor na to pitanje je ne. Pogledajmo primer "lupetanje 2", i dodajmo na desnu stranu te jednačine proizvoljnu konstantu. Očigledno je da na ovaj način dobijamo sasvim novi sistem, što nam obezbeđuje beskonačnost rešenja. Naravno, ne moramo se ograničavati samo na jednačine ovog tipa, možemo se iživljavati koliko god hoćemo, evo za ilustraciju nešto čime sam se danas igrao:
Nastaviti niz
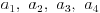
.
Evo, neka je naša rekurentna formula ovakva:
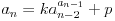
Znači, naš sistem (dve jednačine sa dve nepoznate) izgleda ovako:
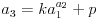
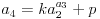
Pretpostavljam da svako zna da reši ovaj sistem po k i p (npr. iz prve jednačine jednostavno izrazimo p i uvrstimo u drugu), i kao rešenja dobijemo sledeću zavisnost:
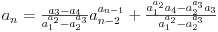
Možemo probati i konkretan primer, npr. niz 1, 2, 3, 4, i dobijemo ovu zavisnost:
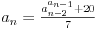
A tek ako ubacimo i trigonometrijske funkcije... Ostavljam vas da se sami igrate koliko želite

Ljubičice crvena, što si plava kô zelena trava.