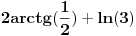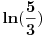Citat:
Ostaje da se pokaze da je C<0.0001, sto nije tesko ako se uoci da je
prva podintegralna funkcija konveksna tako da je povrsina C manja od
povrsine trougla koga cine tacke (3,3) i mesta gde prva podintegralna
funkcija sece prave x=3 i y=3. Malo sam varao pa sam polozaje ove dve
tacke sracunao digitronom i ustanovio da je povrsina trouglica manja od
0.5 * 0.01 *0.01 (oba odsecka su strogo manja od 0.01), tako da je to
zaista manje od jednog stotog dela. S druge strane C je jos i manje od
toga, pa je zbir integrala stvarno manji od 9.0001 cime je dokazan i
"desni" deo nejednakosti
Medutim, racunanje vrednosti odsecaka svodi se tu i tamo na duplo
racunanje kvadratnog korena sto se moze i peske, tako da valjda nisam
previse "zgresio".
Odlicno obavljen posao. Evo, ako ne zamerate, samo da dodam jednu
komplikaciju. Dakle, onaj mali ulubljeni trougao koji ostane se moze naci
kao:
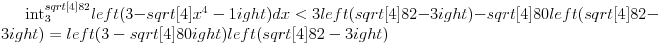
E, sad, posto su oba izraza u zagradama manji od 0.01 (lako se pokaze da je
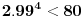
i da je
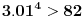
, onda je i njihov
proizvod manji od 0.0001.
Sto se Blazinog zadatka tice, za druge dve sume se dobije "mali milion"
integrala, od kojih se mnogi posle sabiranja resenja za obe sume pokrate,
tako da se na kraju dobije:
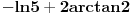
Kad se to sabere sa Brankovim sumama, dobija se
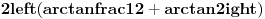
, a to je upravo
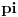
(primenite adicionu formulu za zbir tangensa, nadete inverz od
dobijene vrednosti, i na kraju pomnozite sa dva).
Re: Evo vraski teskih (cisto matematickih) zadataka
