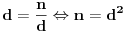Broj delioca prirodnog broja

[ Pregleda: 7526 | Odgovora: 2 ] > FB > Twit

Autor

Goran Arandjelovic
Beograd

Član broj: 29116
Poruke: 387
*.178.EUnet.yu.

+9 Profil

^{20.01.2006. u 14:36 - pre 234 meseci}

Jedno (verovatno glupo) pitanje:

Da li prirodan broj koji nije potpun kvadrat mora da ima paran broj delioca?

Unapred hvala.

Farenhajt
Goran Kapetanović
Beograd

Član broj: 78132
Poruke: 449
*.tehnicom.net.

+6 Profil

^{20.01.2006. u 14:57 - pre 234 meseci}

Mora. Ako prirodan broj predstavimo kao

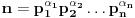
, gde su

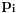
prosti činioci, a

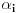
odgovarajući eksponenti, onda je broj njegovih delilaca dat sa

.

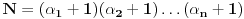
Pretpostavimo prvo da broj nije potpun kvadrat. To znači da je bar jedan eksponent u faktorizaciji neparan, pa će, kad mu se doda

, postati paran i time učiniti parnim čitav proizvod

.

Obratno, ako je proizvod

paran, to znači da je bar jedan od činilaca

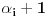
paran, te je odgovarajuće

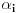
neparno. Samim tim, ni broj

ne može biti pun kvadrat.

Dakle, dokazali smo "ako i samo ako".

Malo jednostavniji rezon glasi ovako: Svaki delilac

prirodnog broja

može se spariti s deliocem

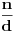
, što znači da će ukupan broj delilaca biti paran ako i samo ako ni za jedan delilac ne važi

Goran Arandjelovic
Beograd

Član broj: 29116
Poruke: 387
*.178.EUnet.yu.

+9 Profil

^{20.01.2006. u 15:05 - pre 234 meseci}

Hvala još jednom.:)

[ Pregleda: 7526 | Odgovora: 2 ] > FB > Twit

Srodne teme

Navigacija

Brisanje liste

Lista poslednjih: 16, 32, 64, 128 poruka.